Introduction and Motivation

I recently decided to work through Hernan and Robbins' textbook, titled: "What If: Causal Inference". While I had gone through some of the basics of Causal Inference (CI) in an epidemiology class required by my curriculum, it didn't have the same level of symbolic logic or mathematical formalism that I had grown to feel more comfortable with in my statistics training. Furthermore, as I push ever further into the realm of observational data it has become increasingly important to me to understand the exact assumptions that I am making or relying on when I write about the results of a specific model. I'm happy to say that I found the book achieved both of those goals and provided much more. While I did find myself occassionally irked by the consistently Frequentist approach, that was a very minor inconvenience and as much a matter of my taste (perhaps) as anything else. As I reached the end of the book, I found myself wanting an excuse to write-up the things I had learned and even sketch out how they applied to my current and future work.

Thus, I intend to write a multi-part blog post series, where each post takes a look at some of the concepts from causal inference. I'm planning to begin very generally, as in the book, reiterating the main principles that allow for valid causal inference to be drawn and then highlight a specific application of a tool for causal inference - Instrumental Variables - in my research. Finally, I'm hoping to apply some of the ideas from the final section of the book, on time varying treatments and confounders, to some general thoughts about how we can understand, plan and evaluate different features of the built environment. If you're interested in learning some basic CI or maybe even just seeing how CI principles are applied in the practice of science I hope you'll enjoy reading what follows. Though the use of some jargon or notation is inevitable, I'll do my best to explain things as they're introduced.

With that introduction out of the way, let's talk about Causal Inference!

Identifiability Conditions

You ordered chocolate ice cream at the ice cream store and you took a simple, post-purchase survey indicating that you liked it, but what if you had gotten vanilla? Would you have liked that just as much? While frozen treats are rarely the intervention of interest, questions like these are common in CI. The problem with trying to answer this question of course, is that you didn't order vanilla ice cream, and so we can't definitively know if you would have liked it. This is called the fundamental problem of Causal Inference, and serves as one of the main obstacles to the project of doing good science. If the objective were to know the affect of some intervention at the level of a single individual we might truly never be able to know, beyond mere speculation, anything about these other potential counterfactual outcomes, that is the outcome - liking the ice cream - that we would have observed under a different or counterfactual setting - getting vanilla instead of chocolate. However, science is typically more concerned with arriving at general truths that are relevant for an entire population,rather than just a single individual. In this case, there are some concepts that can be put to work in order to identify a causal effect. In the literature these are referred to as identifiability conditions. We'll go through each of them briefly to highlight how they can help us identify a causal effect.

Exchangeability

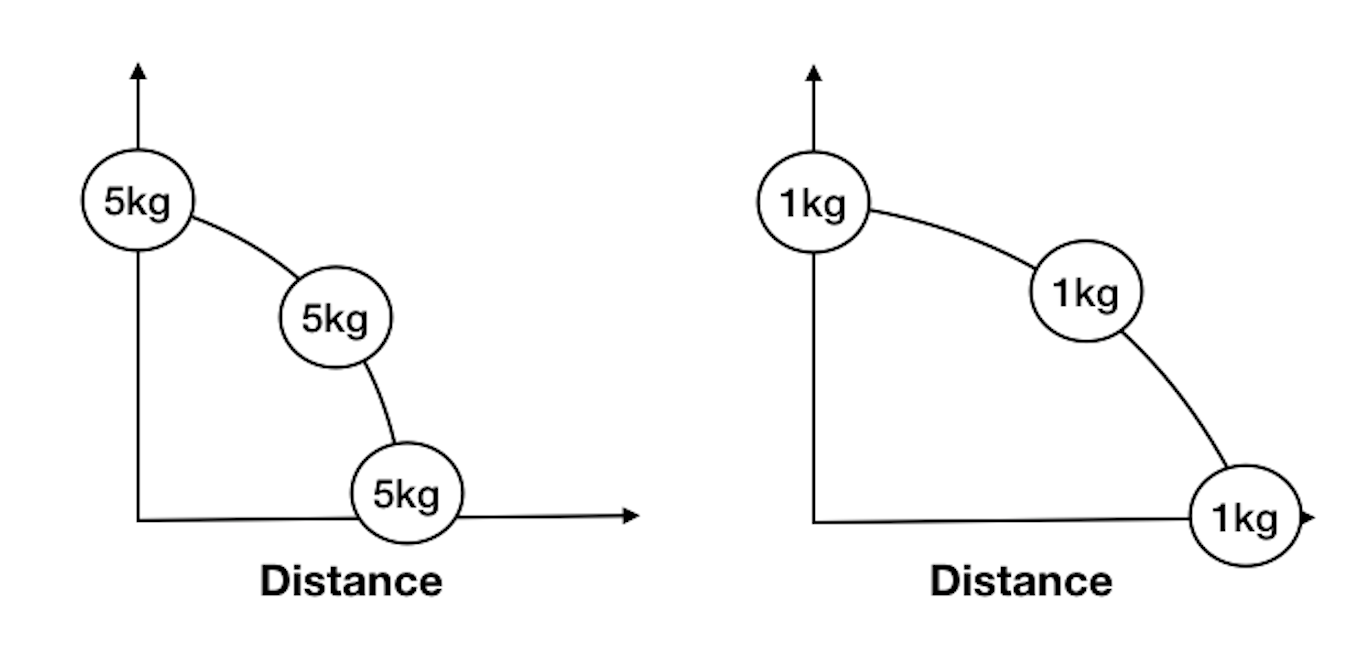
The first of these identifiability conditions is exchangeability. Exchangeability has a formal mathematical definition in probability theory¹ but conceptually, it can be understood as "similarity" or "likeness". To take a rudimentary example from physics, suppose you want to estimate the causal effect of force applied to a ball on that ball's change in position. The hypothesis being that the more force you apply, the greater the change in position². You might imagine that in order to perform this experiment appropriately, you would need to use the same kind of ball each time you applied force to it. If you used a variety of different kinds of balls, where some were lighter or heavier than others, you would expect the change in position to be different for balls of different mass, even though the same force was applied to them. In order to account for this, you would have to include the information - mass - that accounts for the relevant difference between balls change in position. This would create conditional exchangeability between the balls. That is, by conditioning or including the information of each ball's mass, we would be able to make these balls comparable in terms of how force affects their change in position.

In order to identify a causal effect of chocolate/vanilla ice cream on a population's experience at an ice cream store, we would need to assume, before doing any kind of analysis that the individuals at the ice cream store we observe are somehow similar in how ice cream flavor affects their ice cream store experience : that they are exchangeable. We would need to assume two other things too, which I will elaborate on briefly in the next section, as I think they're fairly straightforward concepts.

Positivity and Consistency

Positivity and Consistency refer to the ideas, in the context of our ice cream store example, that we will observe some individuals who have either chocolate or vanilla ice cream (positivity) and that ordering and receiving chocolate or vanilla ice cream means the same thing for every person (consistency). While I think these are both straightforward concepts, it bears mentioning some of the subtlety in how these conditions could be violated. The first, positivity, is violated if no one is observed getting vanilla ice cream, This should make sense intuitively, that it would be impossible to know how people's choice of ordering vanilla ice cream might affect their ice cream store experience if we didn't observe anyone get vanilla ice cream. To be slightly technical, I'll put this in terms of probability below:

\[ P(\text{ice cream choice} = \text{chocolate}) >0 \\ \text{ AND } \\ P(\text{ice cream choice} = \text{vanilla}) > 0. \]

An example in which the condition of consistency might be violated would be if the ice cream store runs out of one brand of vanilla ice cream and end up switching to another, during the period in which we're observing ice cream orders and customers' experience. Suddenly the meaning of "vanilla ice cream" in which we were interested has changed and can no longer be identified as it would be otherwise. Again there are technical definitions here for each of these terms in mathematics that can be found in chapter 3 of Hernan and Robbins' textbook. I'll defer you to look there, so as to keep this subject matter as palatable as possible.

What's Next

If we have subjects that are exchangeable with respect to some intervention or variable of interest and we have positivity and consistency for that variable, then we have the foundation upon which to start drawing valid causal inference. Unfortunately, there are often circumstances that prevent even these assumptions from being met. In the next post I'll write briefly about two common obstacles - Confounding and Selection Bias.